3 Réhaussement et visualisation d’images

Assurez-vous de lire ce préambule avant d’exécutez le reste du notebook.

3.1 Préambule

3.1.1 Objectifs

Dans ce chapitre, nous abordons quelques techniques de réhaussement et de visualisation d’images. Ce chapitre est aussi disponible sous la forme d’un notebook Python:

Objectifs d’apprentissage visés dans ce chapitre

À la fin de ce chapitre, vous devriez être en mesure de :

exploiter les statistiques d’une image pour améliorer la visualisation;
calculer les histogrammes de valeurs;
appliquer une transformation linéaire ou non linéaire pour améliorer une visualisation;
comprendre le principe des composés colorés;

3.1.2 3.1.3 Bibliothèques

Les bibliothèques qui vont être explorées dans ce chapitre sont les suivantes:

Dans l’environnement Google Colab, seul rioxarray et GDAL doivent être installés:

%%capture
!apt-get update
!apt-get install gdal-bin libgdal-dev

Dans l’environnement Google Colab, il convient de s’assurer que les librairies sont installées:

%%capture
!pip install -qU matplotlib rioxarray xrscipy scikit-image

Vérifier les importations:

import numpy as np
import rioxarray as rxr
from scipy import signal
import xarray as xr
import xrscipy
import matplotlib.pyplot as plt

3.1.4 Données

Nous utiliserons les images suivantes dans ce chapitre:

%%capture
import gdown

gdown.download('https://drive.google.com/uc?export=download&confirm=pbef&id=1a6Ypg0g1Oy4AJt9XWKWfnR12NW1XhNg_', output= 'RGBNIR_of_S2A.tif')
gdown.download('https://drive.google.com/uc?export=download&confirm=pbef&id=1a6O3L_abOfU7h94K22At8qtBuLMGErwo', output= 'sentinel2.tif')
gdown.download('https://drive.google.com/uc?export=download&confirm=pbef&id=1_zwCLN-x7XJcNHJCH6Z8upEdUXtVtvs1', output= 'berkeley.jpg')
gdown.download('https://drive.google.com/uc?export=download&confirm=pbef&id=1dM6IVqjba6GHwTLmI7CpX8GP2z5txUq6', output= 'SAR.tif')
gdown.download('https://drive.google.com/uc?export=download&confirm=pbef&id=1a4PQ68Ru8zBphbQ22j0sgJ4D2quw-Wo6', output= 'landsat7.tif')

Vérifiez que vous êtes capable de les lire :

with rxr.open_rasterio('berkeley.jpg', mask_and_scale= True) as img_rgb:
    print(img_rgb)
with rxr.open_rasterio('sentinel2.tif', mask_and_scale= True) as img_s2:
    print(img_s2)
with rxr.open_rasterio('RGBNIR_of_S2A.tif', mask_and_scale= True) as img_rgbnir:
    print(img_rgbnir)
with rxr.open_rasterio('SAR.tif', mask_and_scale= True) as img_SAR:
    print(img_SAR)

3.2 Visualisation en Python

ID’emblée, il faut mentionner que Python n’est pas vraiment fait pour visualiser de la donnée de grande taille, le niveau d’interactivité est aussi assez limité. Pour une visualisation interactives, il est plutôt conseillé d’utiliser un outil comme QGIS. Néanmoins, il est possible de visualiser de petites images avec la librairie matplotlib qui est la librairie principale de visualisation en Python. Cette librairie est extrêmement riche et versatile, nous ne présenterons que les bases nécessaires pour démarrer. Le lecteur désirant aller plus loin pourra consulter les nombreux tutoriels disponibles comme celui-ci.

La fonction de base pour créer une figure est subplots, la largeur et la hauteur en pouces de la figure peuvent être contrôlées via le paramètre figsize:

import matplotlib.pyplot as plt
fig, ax= plt.subplots(figsize=(5, 4))
plt.show()

Pour l’affichage des images, la fonction imshow permet d’afficher une matrice 2D à une dimension en format float ou une matrice RVB avec 3 bandes. Il est important que les dimensions de la matrice soient dans l’ordre hauteur, largeur et bande.

import matplotlib.pyplot as plt
fig, ax= plt.subplots(figsize=(6, 5))
plt.imshow(img_rgbnir[0].data)
plt.show()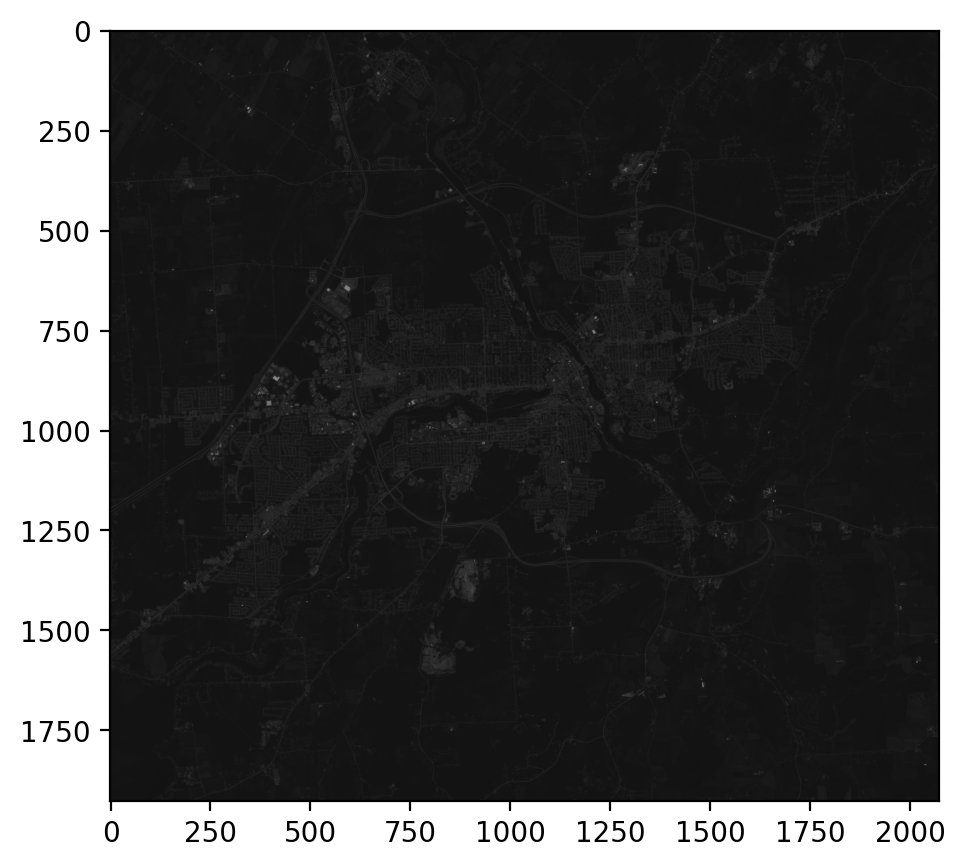

Pour un affichage à trois bandes, les valeurs seront ramenées sur une échelle de 0 à 1, il est donc nécessaire de normaliser les valeurs avant l’affichage:

import matplotlib.pyplot as plt
fig, ax= plt.subplots(figsize=(6, 5))
plt.imshow(img_rgbnir.data.transpose(1,2,0)/2500.0)
plt.show()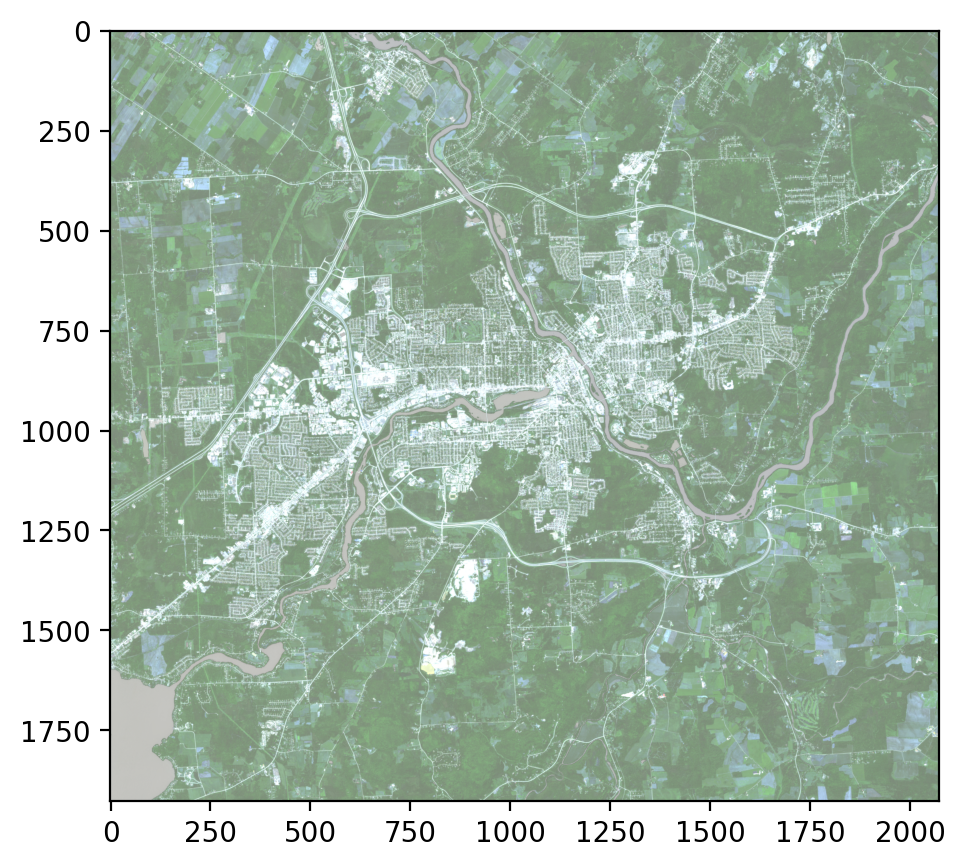

On remarquera les valeurs des axes x et y avec une origine en haut à gauche. Ceci est un référentiel purement matriciel (lignes et colonnes); autrement dit, il n’y a pas ici de géoréférence. Pour pallier à cette limitation, les librairies rasterio et xarray proposent une extension de la fonction imshow permettant d’afficher les coordonnées cartographiques ainsi qu’un contrôle la dynamique de l’image:

import rioxarray as rxr
fig, ax= plt.subplots(figsize=(6, 5))
img_rgbnir.sel(band=[1,2,3]).plot.imshow(vmin=86, vmax=5000)
ax.set_title('Imshow avec rioxarray')
plt.show()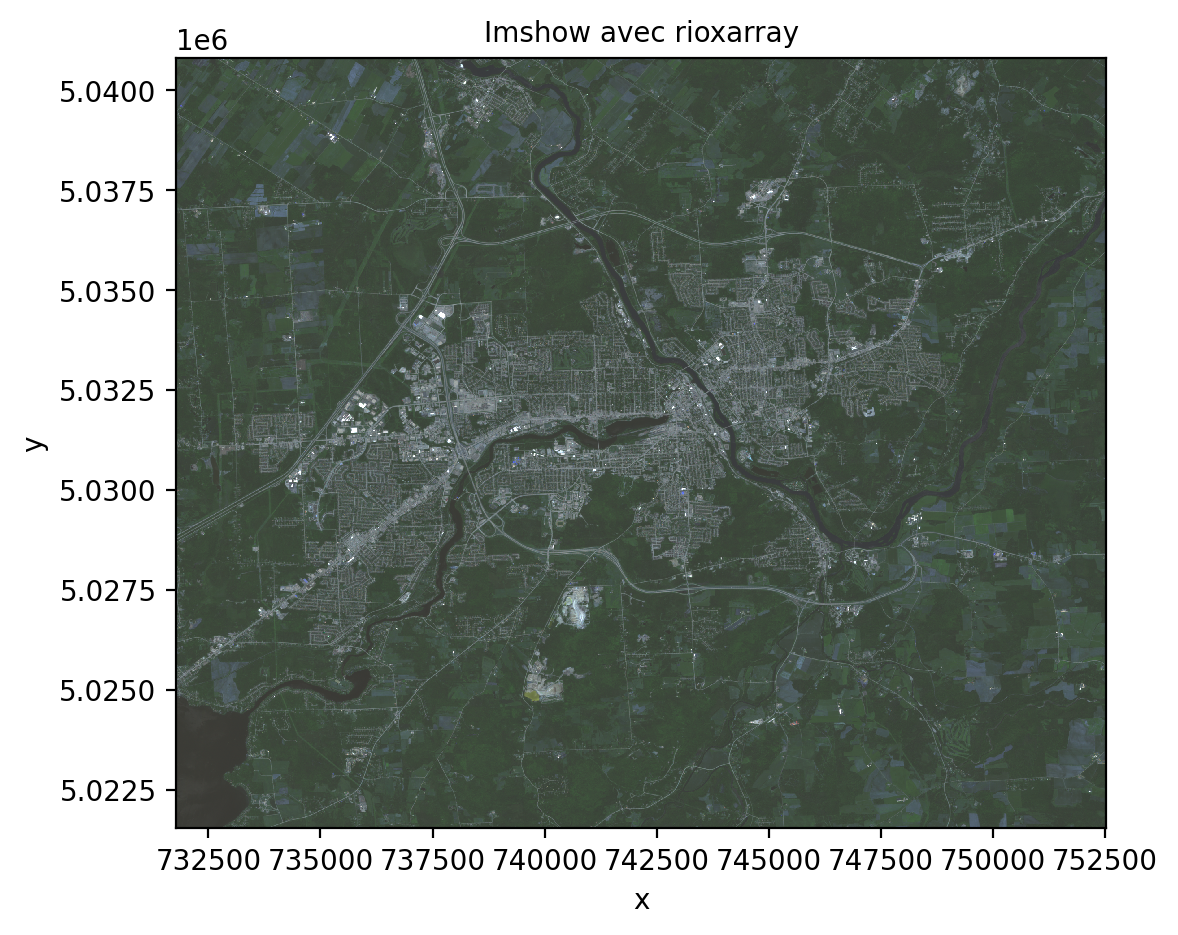

3.3 Réhaussements visuels

Le réhaussement visuel d’une image vise principalement à améliorer la qualité visuelle d’une image en améliorant le contraste, la dynamique ou la texture d’une image. De manière générale, ce réhaussement ne modifie pas la donnée d’origine mais il est appliquée dynamiquement à l’affichage pour des fins d’inspection visuelle. Le réhaussement nécessite généralement une connaissance des caractéristiques statistiques d’une image. Ces statistiques sont ensuite exploitées pour appliquer diverses transformations linéaires ou non linéaires.

3.3.1 Statistiques d’une image

On peut considérer un ensemble de statistique pour chacune des bandes d’une image:

valeurs minimales et maximales
valeurs moyennes,
Quartiles (1er quartile, médiane et 3ième quartile), quantiles et percentiles.
écart-type, et coefficients d’asymétrie (skewness) et d’applatissement (kurtosis)

Ces statistiques doivent être calculées pour chaque bande d’une image multispectrale.

En ligne de commande, gdalinfo permet d’interroger rapidement un fichier image pour connaitre ces statistiques univariées de base:

!gdalinfo -stats landsat7.tif

Driver: GTiff/GeoTIFF
Files: landsat7.tif
       landsat7.tif.aux.xml
Size is 2181, 1917
Coordinate System is:
PROJCS["WGS 84 / Pseudo-Mercator",
    GEOGCS["WGS 84",
        DATUM["WGS_1984",
            SPHEROID["WGS 84",6378137,298.257223563,
                AUTHORITY["EPSG","7030"]],
            AUTHORITY["EPSG","6326"]],
        PRIMEM["Greenwich",0,
            AUTHORITY["EPSG","8901"]],
        UNIT["degree",0.0174532925199433,
            AUTHORITY["EPSG","9122"]],
        AUTHORITY["EPSG","4326"]],
    PROJECTION["Mercator_1SP"],
    PARAMETER["central_meridian",0],
    PARAMETER["scale_factor",1],
    PARAMETER["false_easting",0],
    PARAMETER["false_northing",0],
    UNIT["metre",1,
        AUTHORITY["EPSG","9001"]],
    AXIS["X",EAST],
    AXIS["Y",NORTH],
    EXTENSION["PROJ4","+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext +no_defs"],
    AUTHORITY["EPSG","3857"]]
Origin = (-13651650.000000000000000,4576290.000000000000000)
Pixel Size = (30.000000000000000,-30.000000000000000)
Metadata:
  AREA_OR_POINT=Area
  OVR_RESAMPLING_ALG=NEAREST
  TIFFTAG_RESOLUTIONUNIT=1 (unitless)
  TIFFTAG_XRESOLUTION=1
  TIFFTAG_YRESOLUTION=1
Image Structure Metadata:
  COMPRESSION=DEFLATE
  INTERLEAVE=PIXEL
Corner Coordinates:
Upper Left  (-13651650.000, 4576290.000) (122d38' 5.49"W, 37d58'40.08"N)
Lower Left  (-13651650.000, 4518780.000) (122d38' 5.49"W, 37d34'10.00"N)
Upper Right (-13586220.000, 4576290.000) (122d 2'49.53"W, 37d58'40.08"N)
Lower Right (-13586220.000, 4518780.000) (122d 2'49.53"W, 37d34'10.00"N)
Center      (-13618935.000, 4547535.000) (122d20'27.51"W, 37d46'26.05"N)
Band 1 Block=512x512 Type=Byte, ColorInterp=Red
  Min=19.000 Max=233.000 
  Minimum=19.000, Maximum=233.000, Mean=98.433, StdDev=21.164
  NoData Value=0
  Overviews: 1091x959, 546x480
  Metadata:
    STATISTICS_MAXIMUM=233
    STATISTICS_MEAN=98.433096940153
    STATISTICS_MINIMUM=19
    STATISTICS_STDDEV=21.164021026458
Band 2 Block=512x512 Type=Byte, ColorInterp=Green
  Min=19.000 Max=178.000 
  Minimum=19.000, Maximum=178.000, Mean=55.068, StdDev=22.204
  NoData Value=0
  Overviews: 1091x959, 546x480
  Metadata:
    STATISTICS_MAXIMUM=178
    STATISTICS_MEAN=55.067787534804
    STATISTICS_MINIMUM=19
    STATISTICS_STDDEV=22.203571974581
Band 3 Block=512x512 Type=Byte, ColorInterp=Blue
  Min=19.000 Max=187.000 
  Minimum=19.000, Maximum=187.000, Mean=43.341, StdDev=20.330
  NoData Value=0
  Overviews: 1091x959, 546x480
  Metadata:
    STATISTICS_MAXIMUM=187
    STATISTICS_MEAN=43.340507443056
    STATISTICS_MINIMUM=19
    STATISTICS_STDDEV=20.32987736339

Les librairies de base comme rasterio et xarray produisent facilement un sommaire des statistiques de base avec la fonction stats:

import rasterio as rio
import numpy as np
with rio.open('landsat7.tif') as src:
    stats= src.stats()
    print(stats)

La librairie xarray donne accès à des fonctionnalités plus sophistiquées comme le calcul des quantiles:

import rioxarray as riox
with riox.open_rasterio('landsat7.tif', masked= True) as src:
    print(src)
quantiles = src.quantile(dim=['x','y'], q=[.025,.25,.5,.75,.975])
quantiles

<xarray.DataArray (band: 3, y: 1917, x: 2181)> Size: 50MB
[12542931 values with dtype=float32]
Coordinates:
  * band         (band) int64 24B 1 2 3
  * x            (x) float64 17kB -1.365e+07 -1.365e+07 ... -1.359e+07
  * y            (y) float64 15kB 4.576e+06 4.576e+06 ... 4.519e+06 4.519e+06
    spatial_ref  int64 8B 0
Attributes:
    AREA_OR_POINT:           Area
    OVR_RESAMPLING_ALG:      NEAREST
    TIFFTAG_RESOLUTIONUNIT:  1 (unitless)
    TIFFTAG_XRESOLUTION:     1
    TIFFTAG_YRESOLUTION:     1
    STATISTICS_MAXIMUM:      233
    STATISTICS_MEAN:         98.433096940153
    STATISTICS_MINIMUM:      19
    STATISTICS_STDDEV:       21.164021026458
    scale_factor:            1.0
    add_offset:              0.0

3.3.1.1 Calcul de l’histogramme

Le calcul d’un histogramme pour une image (une bande) permet d’avoir une vue plus détaillée de la répartition des valeurs radiométriques. Le calcul d’un histogramme nécessite minimalement de faire le choix du nombre de barre ( bins ou de la largeur ). Un bin est un intervalle de valeurs pour lequel on peut calculer le nombre de valeurs observées dans l’image. La fonction de base pour ce type de calcul est la fonction numpy.histogram():

import numpy as np
array = np.random.randint(0,10,100) # 100 valeurs aléatoires entre 0 et 10
hist, bin_limites = np.histogram(array, density=True)
print('valeurs :',hist)
print(';imites :',bin_limites)

valeurs : [0.1        0.07777778 0.07777778 0.08888889 0.16666667 0.12222222
 0.05555556 0.13333333 0.14444444 0.14444444]
;imites : [0.  0.9 1.8 2.7 3.6 4.5 5.4 6.3 7.2 8.1 9. ]

Le calcul se fait avec 10 intervalles par défaut.

fig, ax= plt.subplots(figsize=(5, 4))
plt.bar(bin_limites[:-1],hist)
plt.show()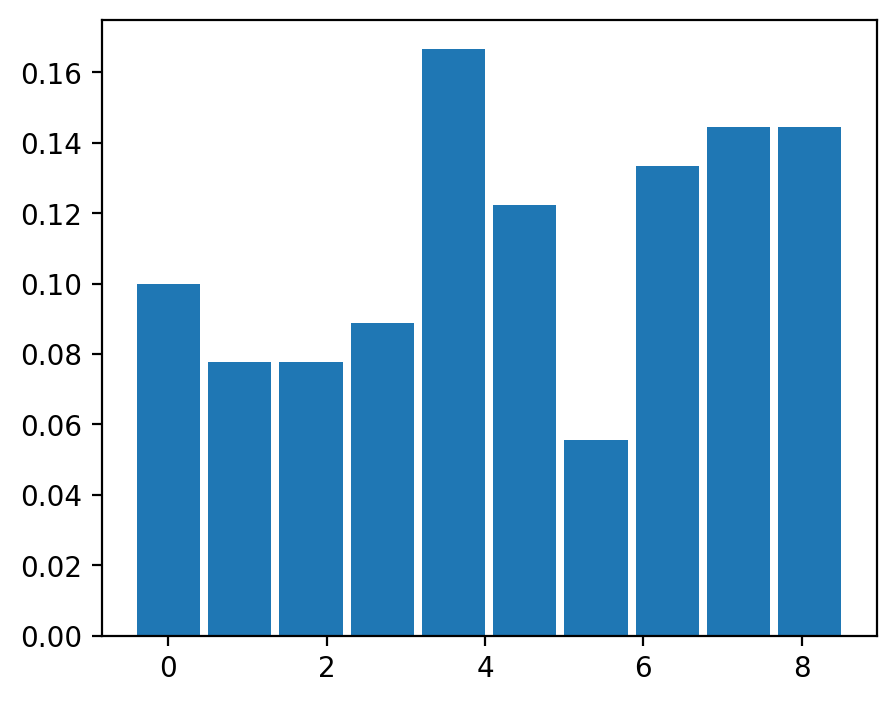

Pour des besoins de visualisation, le calcul des valeurs extrêmes de l’histogramme peut aussi se faire via les quantiles comme discutés auparavant.

3.3.1.1.1 Visualisation des histogrammes

La librarie rasterio est probablement l’outil le plus simples pour visualiser rapidement des histogrammes sur une image multi-spectrale:

import rasterio as rio
from rasterio.plot import show_hist
with rio.open('RGBNIR_of_S2A.tif') as src:
  show_hist(src, bins=50, lw=0.0, stacked=False, alpha=0.3,histtype='stepfilled', title="Histogram")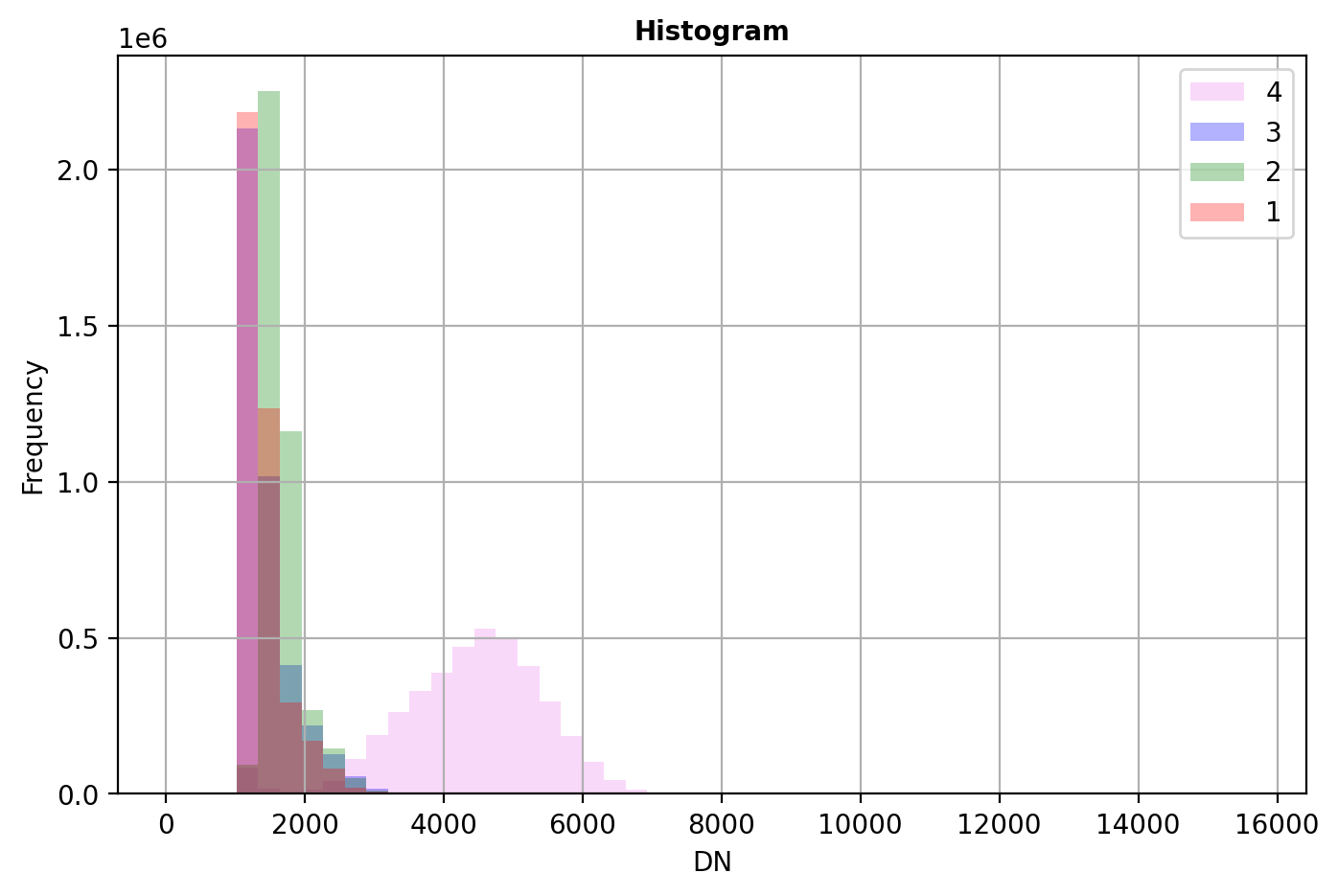

3.3.2 Réhaussements linéaires

Le réhaussement linéaire (linear stretch) d’une image est la forme la plus simple de réhaussement, elle consiste à 1) optimiser les valeurs des pixels d’une image afin de maximiser la dynamique disponibles à l’affichage, ou 2) à changer le format de stockage des valeurs (de 8 bits à 16 bits):

\[ \text{nouvelle valeur d'un pixel} = \frac{\text{valeur d'un pixel} - min_0}{max_0 - min_0}\times (max_1 - min_1)+min_1 \tag{3.1}\]

Par cette opération, on passe de la dynamique de départ (\(max_0 - min_0\)) vers la dynamique cible (\(max_1 - min_1\)). Bien que cette opération semble triviale, il est important d’être conscient des trois contraintes suivantes:

Faire attention à la dynamique cible, ainsi, pour sauvegarder une image en format 8 bit, on utilisera alors \(max_1=255\) et \(min_1=0\).

2. Préservation de la valeur de no data : il faut faire attention à la valeur \(min_1\) dans le cas d’une valeur présente pour no_data. Par exemple, si no_data=0 alors il faut s’assurer que \(min_1>0\).

3. Précision du calcul : si possible réaliser la division ci-dessus en format float

3.3.2.1 Cas des histogrammes asymétriques

Dans certains cas, la distribution de valeurs est très asymétrique et présente une longue queue avec des valeurs extrêmes élevées (à droite ou à gauche de l’histogramme). Le cas des images SAR est particulièrement représentatif de ce type de données. En effet, celles-ci peuvent présenter une distribution de valeurs de type exponentiel. Il est alors préférable d’utiliser des percentiles au préalable afin d’explorer la forme de l’histogramme et la distribution des valeurs:

NO_DATA_FLOAT= -999.0
# on prend tous les pixels de la première bande
values = img_SAR[0].values.flatten().astype(float)
# on exclut les valeurs invalides
values = values[~np.isnan(values)]
# on exclut le no data
values = values[values!=NO_DATA_FLOAT]
# calcul des percentiles
percentiles_position= (0,0.1,1,2,50,98,99,99.9,100)
percentiles= dict(zip(percentiles_position, np.percentile(values, percentiles_position)))
print(percentiles)

{0: np.float64(8.172580237442162e-06), 0.1: np.float64(1.588739885482937e-05), 1: np.float64(8.657756850880105e-05), 2: np.float64(0.00018846066552214325), 50: np.float64(0.012372820172458887), 98: np.float64(0.1719470709562302), 99: np.float64(0.27963151514529694), 99.9: np.float64(1.5235805057287233), 100: np.float64(483.223876953125)}

On constate que la valeur médiane (0.012) est très faible, ce qui signifie que 50% des valeurs sont inférieures à cette valeur alors que la valeur maximale (483) est 10 000 fois plus élevée! Une manière de visualiser cette distribution de valeurs est d’utiliser boxplot et violinplot de la librairie matplotlib:

fig, ax = plt.subplots(nrows=2, ncols=1, figsize=(6, 4), sharex=True)
ax[0].set_title('Distribution de la bande 0 de img_SAR', fontsize='small')
ax[0].grid(True)
ax[0].violinplot(values, orientation  ='horizontal', 
                 quantiles =(0.01,0.02,0.50,0.98,0.99),
                  showmeans=False,
                  showmedians=True)
ax[1].set_xlabel('Valeur des pixels')
ax[1].grid(True)
bplot = ax[1].boxplot(values, notch = True, orientation  ='horizontal')
plt.tight_layout()
plt.show()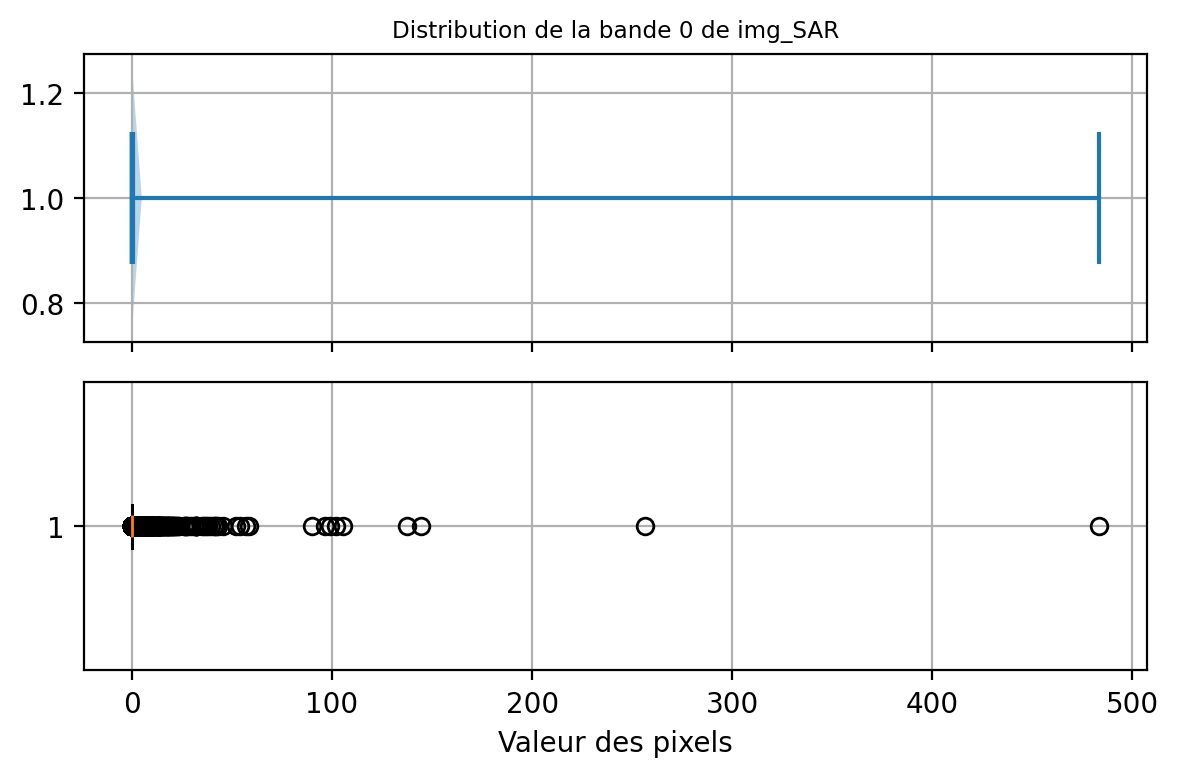

Afin de visualiser correctement l’histogramme, il faut se limiter à un intervalle de valeurs plus réduit. Dans le code ci-dessous, on impose à la fonction np.histogramme de compter les valeurs de pixels dans des intervalles de valeurs fixés par la fonction np.linspace(percentiles[0.1],percentiles[99.9], 50) où percentiles[0.1] et percentiles[99.9] sont les \(0.1\%\) et \(99.9\%\) percentiles respectivement:

hist, bin_edges = np.histogram(values, 
                                bins=np.linspace(percentiles[0.1], 
                                percentiles[99.9], 50), 
                                density=True)

fig, ax = plt.subplots(nrows=2,ncols=1,figsize=(6, 5), sharex=True)
ax[0].bar(bin_edges[:-1], 
                hist*(bin_edges[1]-bin_edges[0]), 
                width= (bin_edges[1]-bin_edges[0]), 
                edgecolor= 'w')
ax[0].set_title("Distribution de probabilité (PDF)")
ax[0].set_ylabel("Densité de probabilité")
ax[0].grid(True)

ax[1].plot(bin_edges[:-1], 
            hist.cumsum()*(bin_edges[1]-bin_edges[0]))
ax[1].set_title("Distribution de probabilité cumulée (CDF)")
ax[1].set_xlabel("Valeur du pixel")
ax[1].set_ylabel("Probabilité cumulée")
ax[1].grid(True)
plt.tight_layout()
plt.show()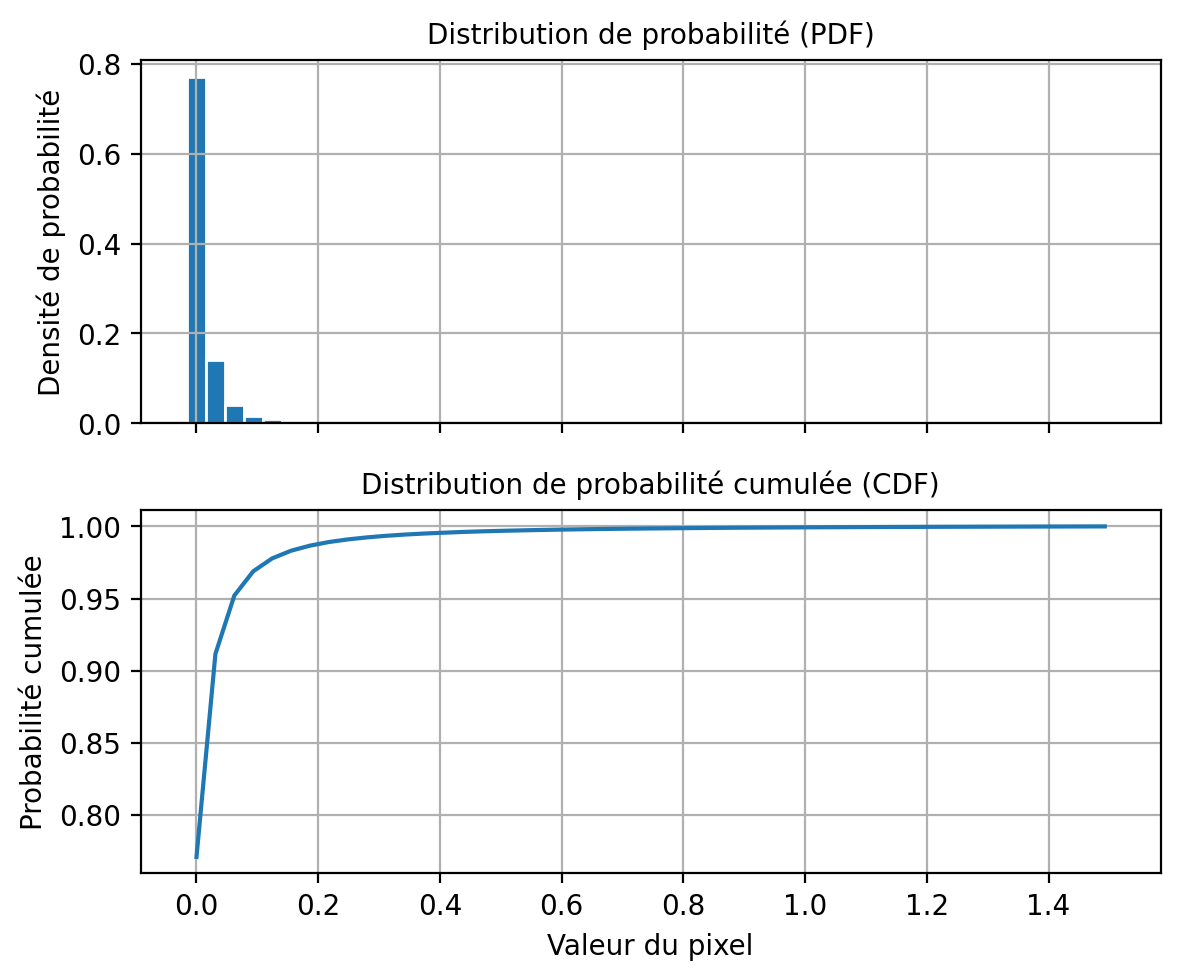

Au niveau de l’affichage avec matplotlib, la dynamique peut être contrôlée directement avec les paramètres vmin et vmax comme ceci:

fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(6, 5), sharex=True, sharey=True)
[a.axis('off') for a in ax.flatten()]
ax[0,0].imshow(img_SAR[0].values, vmin=percentiles[0], vmax=percentiles[100])
ax[0,0].set_title(f"0% - 100%={percentiles[0]:2.1f} - {percentiles[100]:2.1f}")
ax[0,1].imshow(img_SAR[0].values, vmin=percentiles[0.1], vmax=percentiles[99.9]) 
ax[0,1].set_title(f"0.1% - 99.9%={percentiles[0.1]:2.1f} - {percentiles[99.9]:2.1f}")
ax[1,0].imshow(img_SAR[0].values, vmin=percentiles[1], vmax=percentiles[99]) 
ax[1,0].set_title(f"1% - 99%={percentiles[1]:2.1f} - {percentiles[99]:2.1f}")
ax[1,1].imshow(img_SAR[0].values, vmin=percentiles[2], vmax=percentiles[98]) 
ax[1,1].set_title(f"2% - 98%={percentiles[2]:2.1f} - {percentiles[98]:2.1f}")
plt.tight_layout()

3.3.3 Réhaussements non linéaires

3.3.3.1 Réhaussement par fonctions

Le réhaussenent par fonction consiste à appliquer une fonction non linéaire afin de modifier la dynamique de l’image. Par exemple, pour une image radar, une transformation populaire est d’afficher les valeurs de rétrodiffusion en décibel (dB) avec la fonction log10().

percentiles_position= (0,0.1,1,2,50,98,99,99.9,100)
values= xr.apply_ufunc(lambda x: 10 * np.log10(x), img_SAR[0]).data
percentiles_db= dict(zip(percentiles_position, np.percentile(values, percentiles_position)))
print(percentiles_db)

{0: np.float64(-50.87641143798828), 0.1: np.float64(-47.98947440338135), 1: np.float64(-40.625951309204105), 2: np.float64(-37.24779266357422), 50: np.float64(-19.075313568115234), 98: np.float64(-7.6460519409179675), 99: np.float64(-5.534139237403945), 99.9: np.float64(1.8286541925668764), 100: np.float64(26.84148406982422)}

Les boites à moustache (boxplots) ont une bien meilleure distribution qui est en effet très proche d’une distribution normale gaussienne:

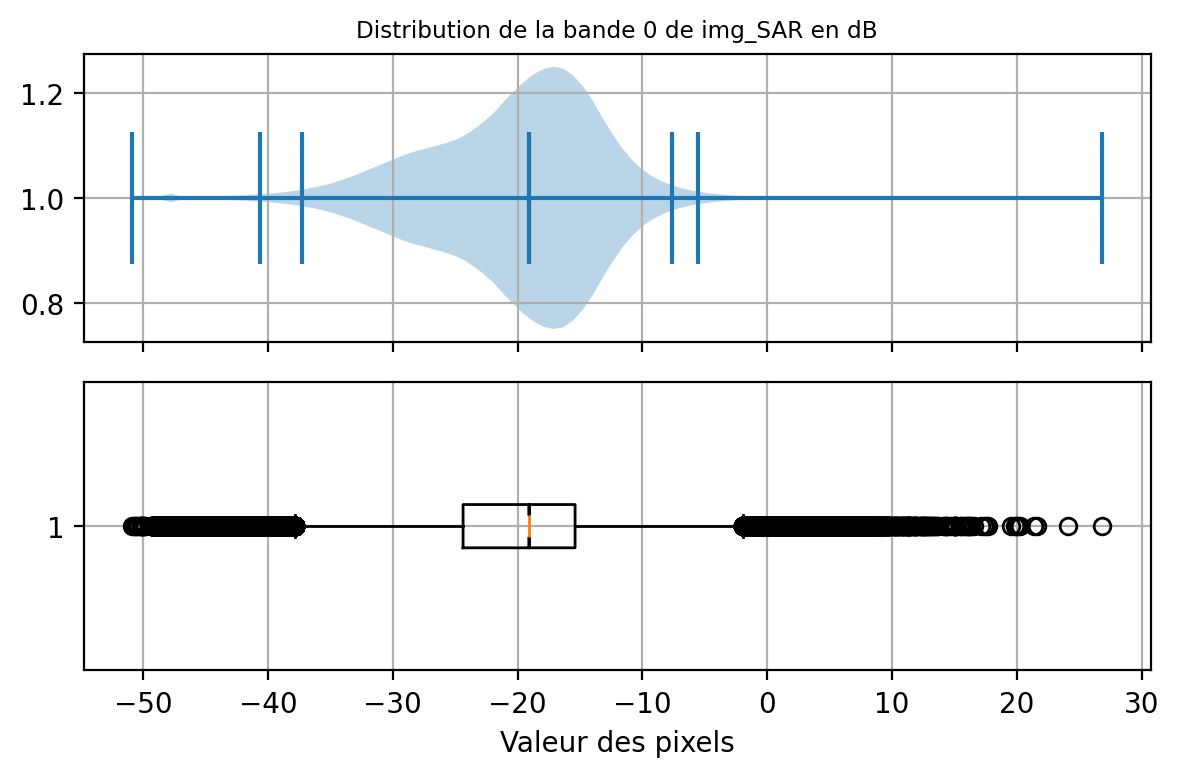
On obtient ainsi les images suivantes:

3.3.3.2 Égalisation d’histogramme

L’égalisation d’histogramme consiste à modifier les valeurs des pixels d’une image source afin que la distribution cumulée des valeurs (CDF) devienne similaire à celle d’une image cible. La CDF (Cumulative Distribution Function) est simplement la somme cumulée des valeurs de l’histogramme:

\[ CDF_{source}(i)= \frac{1}{K}\sum_{j=0}^{j \leq i} hist_{source}(j) \] avec \(K\) choisit de façon à ce que la dernière valeur soit égale à 1 (\(CDF_{source}(i_{max})=1\)). De la même manière, \(CDF_{cible}\) est la CDF d’une image cible. La formule générale pour l’égalisation d’histogramme est la suivante: \[ j = CDF_{cible}^{-1}(CDF_{source}(i)) \]

On peut choisir \(CDF_{cible}\) comme correspondant à une image où chaque valeur de pixel est équiprobable (d’où le terme égalisation), ce qui veut dire \(hist_{cible}(j)=1/L\) avec \(L\) égale au nombre de valeurs possibles dans l’image (par exemple \(L=256\)). \[ j = L \times CDF_{source}(i) \] On peut appliquer cette procédure sur l’image SAR en dB de la façon suivante:

values= np.sort(10*np.log10(img_SAR[0].data.flatten()))
cdf_x= np.linspace(values[0], values[-1], 1000)
cdf_source= np.interp(cdf_x, values, np.arange(len(values))/len(values)*255)
values_eq=np.interp(np.log10(img_SAR[0].data), cdf_x, cdf_source).astype('uint8')
plt.imshow(values_eq)
plt.axis('off')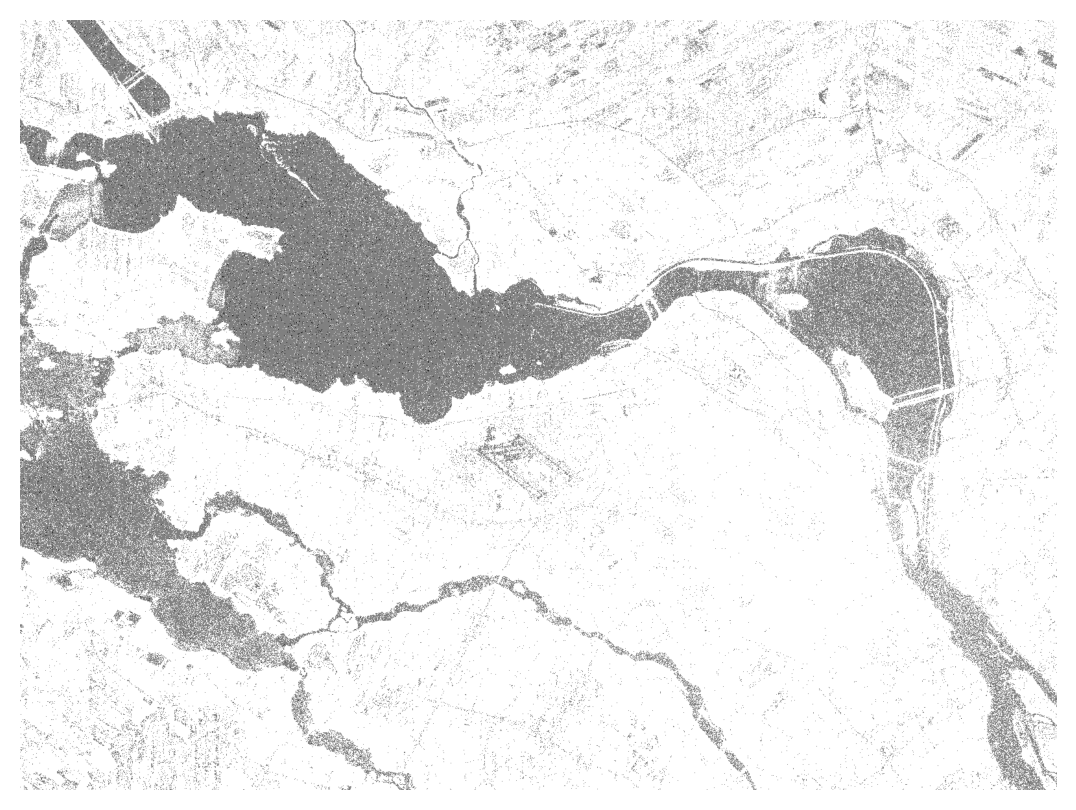

3.3.3.3 Palettes de couleur

Les palettes de couleurs sont appliquées dynamiquement à l’affichage sur une image à une seule bande. La librairie matplotlib contient un nombre considérable de palettes.

from matplotlib import colormaps
list(colormaps)

Voici quelques exemples ci-dessous, les valeurs de l’image doivent être normalisées entre 0 et 1 ou entre 0 et 255 sinon les paramètres vmin et vmax doivent être spécifiés. On peut observer comment ces palettes révèlent les détails de l’image malgré une image originalement très sombre.

fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(6, 5), sharex=True, sharey=True)
[a.axis('off') for a in ax.flatten()]
ax[0,0].imshow(img_SAR[0].data, vmin=percentiles[2], vmax=percentiles[98], cmap='jet')
ax[0,0].set_title(f"jet")
ax[0,1].imshow(img_SAR[0].data, vmin=percentiles[2], vmax=percentiles[98], cmap='hot')
ax[0,1].set_title(f"hot")
ax[1,0].imshow(img_SAR[0].data, vmin=percentiles[2], vmax=percentiles[98], cmap='hsv')
ax[1,0].set_title(f"hsv")
ax[1,1].imshow(img_SAR[0].data, vmin=percentiles[2], vmax=percentiles[98], cmap='terrain')
ax[1,1].set_title(f"terrain")
plt.tight_layout()

Il peut être utile d’ajouter une barre de couleurs afin d’indiquer la correspondance entre les couleurs et les valeurs numériques:

import matplotlib as mpl
fig, ax = plt.subplots(figsize=(6, 6))
cmap= mpl.colormaps.get_cmap('jet').with_extremes(under='white', over='magenta')
h=plt.imshow(img_SAR[0].data, norm=mpl.colors.LogNorm(vmin=percentiles[2], vmax=percentiles[98]),
                   cmap=cmap)
fig.colorbar(h, ax=ax,  orientation='horizontal', label="Intensité", extend='both')
ax.axis('off')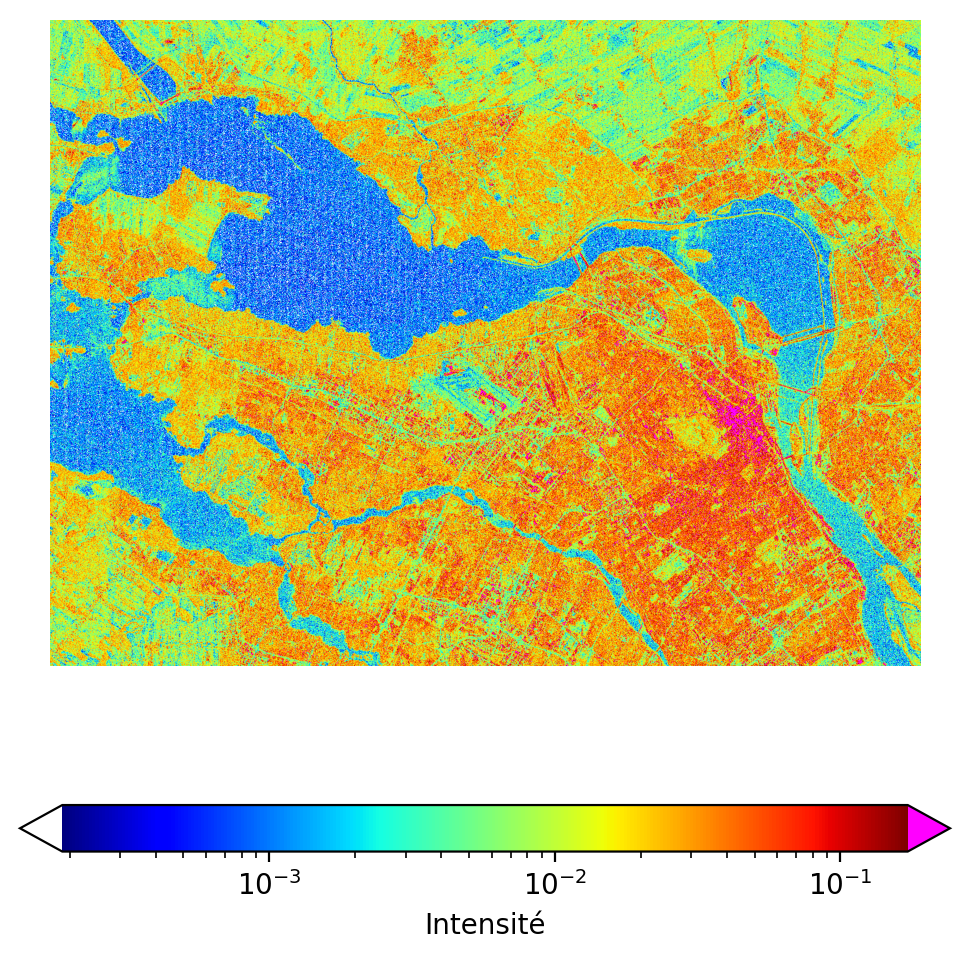

3.3.4 Composés colorés

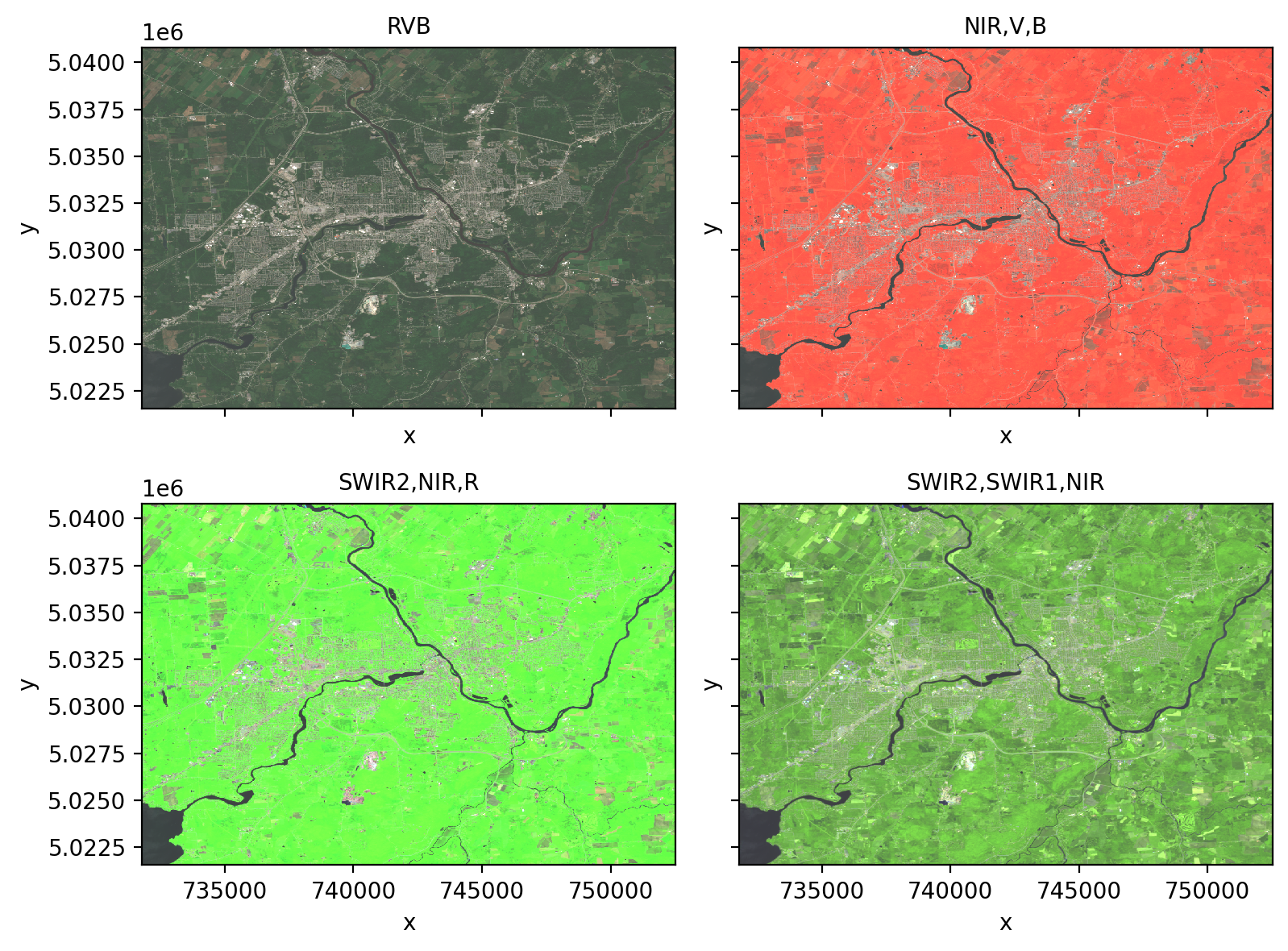
Le système visuel humain est sensible seulement à la partie visible du spectre électromagnétique qui compose les couleurs de l’arc-en-ciel du bleu au rouge. L’ensemble des couleurs du spectre visible peut être obtenu à partir du mélange de trois couleurs primaires (rouge, vert et bleu). Ce système de décomposition à trois couleurs est à la base de la plupart des systèmes de visualisation ou de représentation de l’information de couleur. Si on prend le cas des images Sentinel-2, 12 bandes sont disponibles, plusieurs composés couleurs sont donc possibles (voir le site de Copernicus). Voici quelques exemples possibles, chaque composé mettant en valeur des propriétés différentes de la surface.

import rioxarray as rxr
fig, ax= plt.subplots(nrows=2, ncols= 2, figsize=(8, 6), sharex=True, sharey=True)
img_s2.sel(band=[4,3,2]).plot.imshow(vmin=86, vmax=4000, ax=ax[0,0])
ax[0,0].set_title('RVB')
img_s2.sel(band=[8,3,2]).plot.imshow(vmin=86, vmax=4000, ax=ax[0,1])
ax[0,1].set_title('NIR,V,B')
img_s2.sel(band=[12,8,4]).plot.imshow(vmin=86, vmax=4000, ax=ax[1,0])
ax[1,0].set_title('SWIR2,NIR,R')
img_s2.sel(band=[12,11,4]).plot.imshow(vmin=86, vmax=4000, ax=ax[1,1])
ax[1,1].set_title('SWIR2,SWIR1,NIR')
plt.tight_layout()
plt.show()